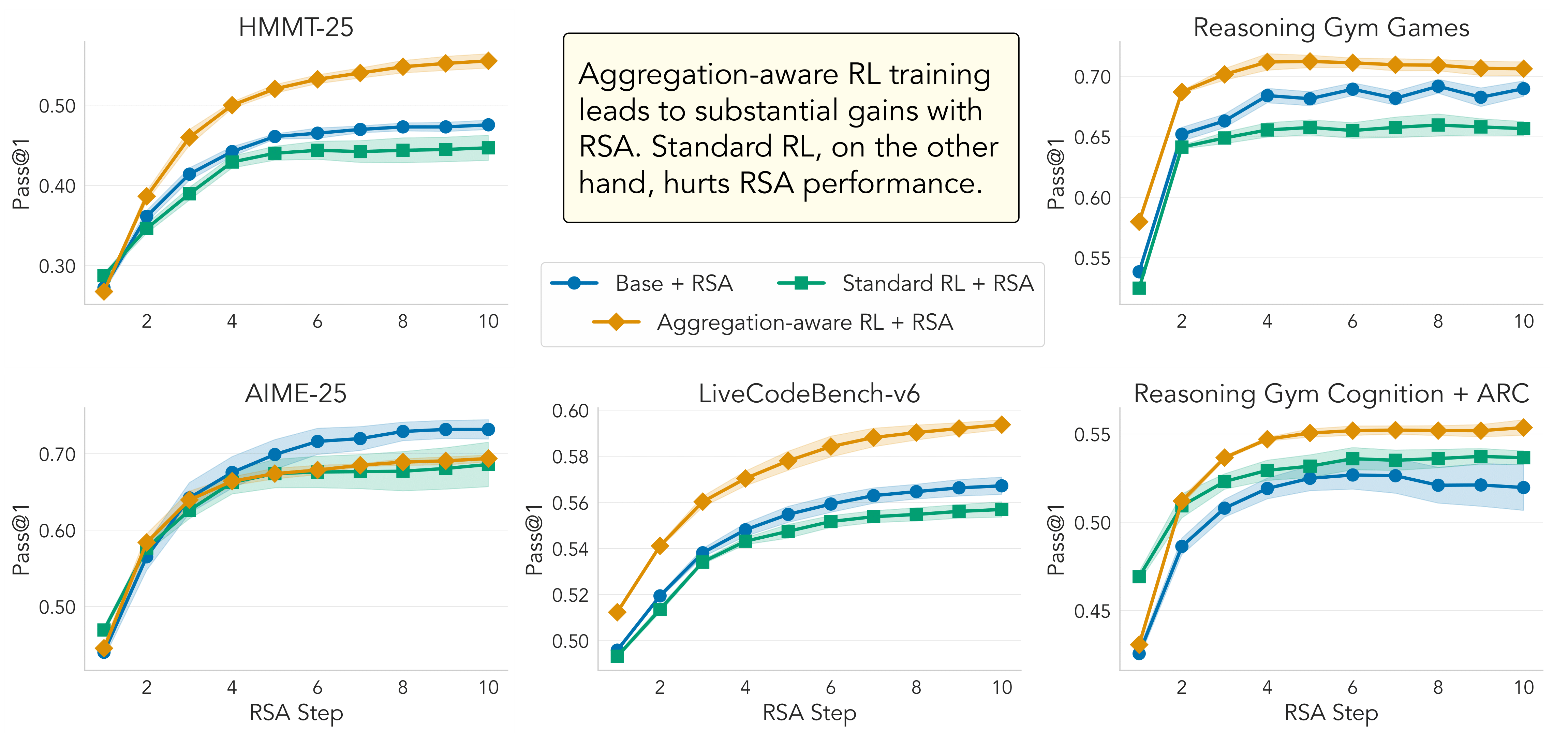
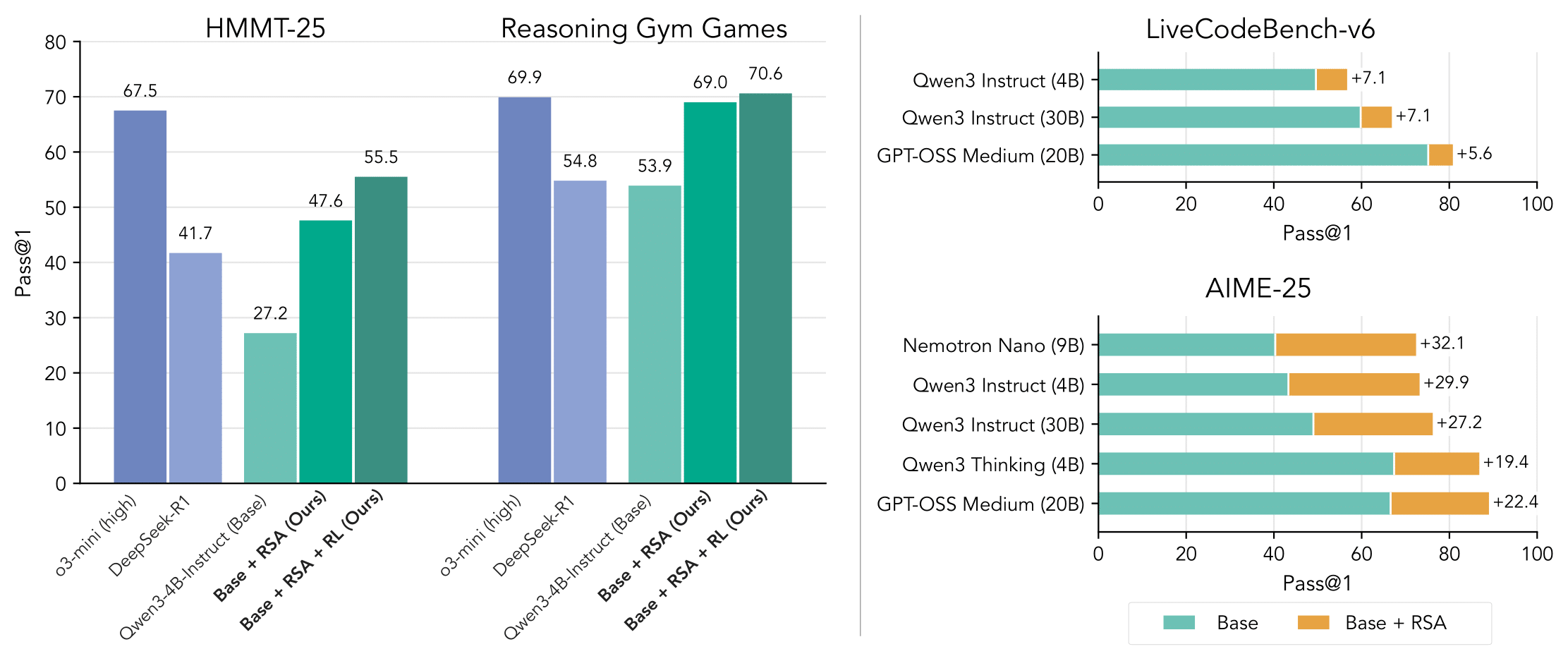Recursive Self-Aggregation Unlocks Deep Thinking in Large Language Models

Venkatraman, Siddarth; Jain, Vineet; Mittal, Sarthak; Shah, Vedant; Obando-Ceron, Johan; Bengio, Yoshua; Bartoldson, Brian; Kailkhura, Bhavya; Lajoie, Guillaume; Berseth, Glen; Malkin, Nikolay; Jain, Moksh

Abstract

Test-time scaling methods improve the capabilities of Large Language Models (LLMs) by increasing the amount of compute used during inference to make a prediction. Inference-time compute can be scaled in parallel by choosing among multiple independent solutions or sequentially through self-refinement. We propose Recursive Self-Aggregation (RSA), a test-time scaling method inspired by evolutionary methods that combines the benefits of both parallel and sequential scaling. Each step of RSA refines a population of candidate reasoning chains through aggregation of subsets to yield a population of improved solutions, which are then used as the candidate pool for the next iteration. RSA exploits the rich information embedded in the reasoning chains -- not just the final answers -- and enables bootstrapping from partially correct intermediate steps within different chains of thought. Empirically, RSA delivers substantial performance gains with increasing compute budgets across diverse tasks, model families and sizes. Notably, RSA enables Qwen3-4B-Instruct-2507 to achieve competitive performance with larger reasoning models, including DeepSeek-R1 and o3-mini (high), while outperforming purely parallel and sequential scaling strategies across AIME-25, HMMT-25, Reasoning Gym, LiveCodeBench-v6, and SuperGPQA. We further demonstrate that training the model to combine solutions via a novel aggregation-aware reinforcement learning approach yields significant performance gains. Code is available here.

Recursive Self-Aggregation

RSA generates a population of $N$ solutions for a given prompt and recursively updates them over $T$ steps. Each step subsamples $K$ distinct solutions from the current population and generates an improved solution.

During post-training, LLMs are trained with reinforcement learning (RL) to improve their reasoning ability. RL training does not account for test-time scaling, which in this case is the task of aggregating multiple reasoning chains. In fact, we observe that standard RL fine-tuning can even degrade performance relative to the base model when combined with test-time aggregation. To address this, we propose an aggregation-aware RL approach using a simple data-augmentation strategy to train LLMs to aggregate solutions.

We present Recursive Self-Aggregation (RSA), a hybrid test-time scaling procedure designed to improve the model's performance without complex scaffolding or using external verifiers. It frames reasoning as a form of evolutionary process where candidate reasoning chains are iteratively refined through self-aggregation, inspired by the crossover and mutation steps in genetic algorithms.

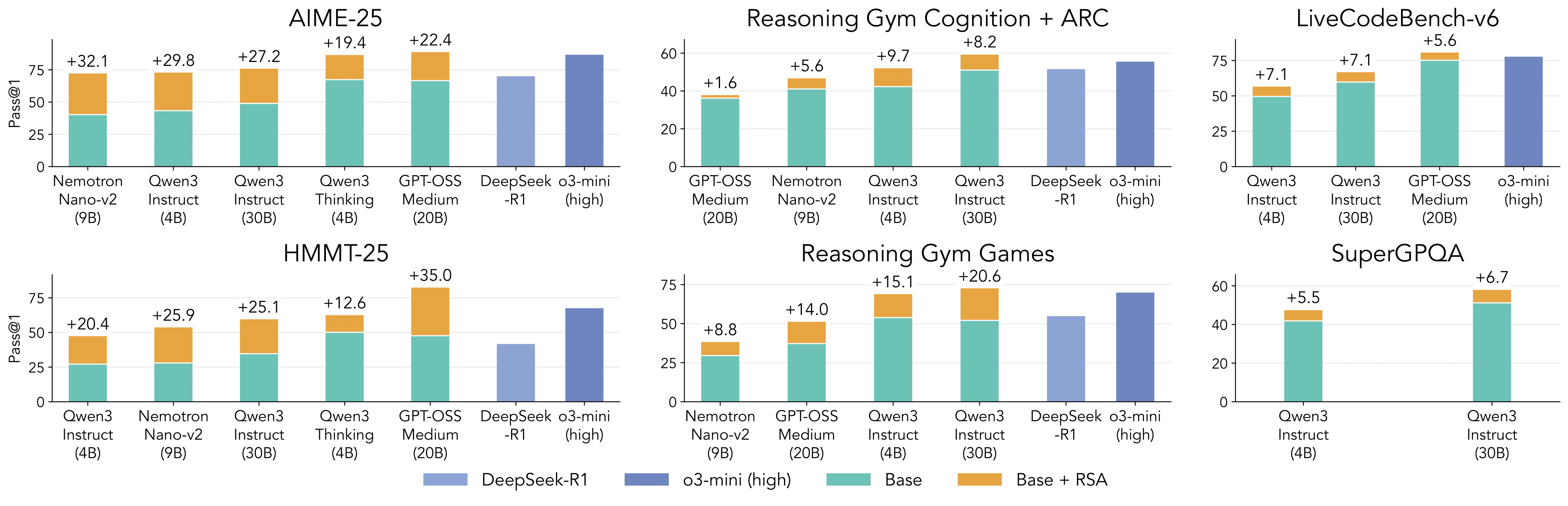
RSA is simple to implement and leads to substantial improvements in reasoning abilities across different models and tasks, when compared to pure sequential or parallel scaling.

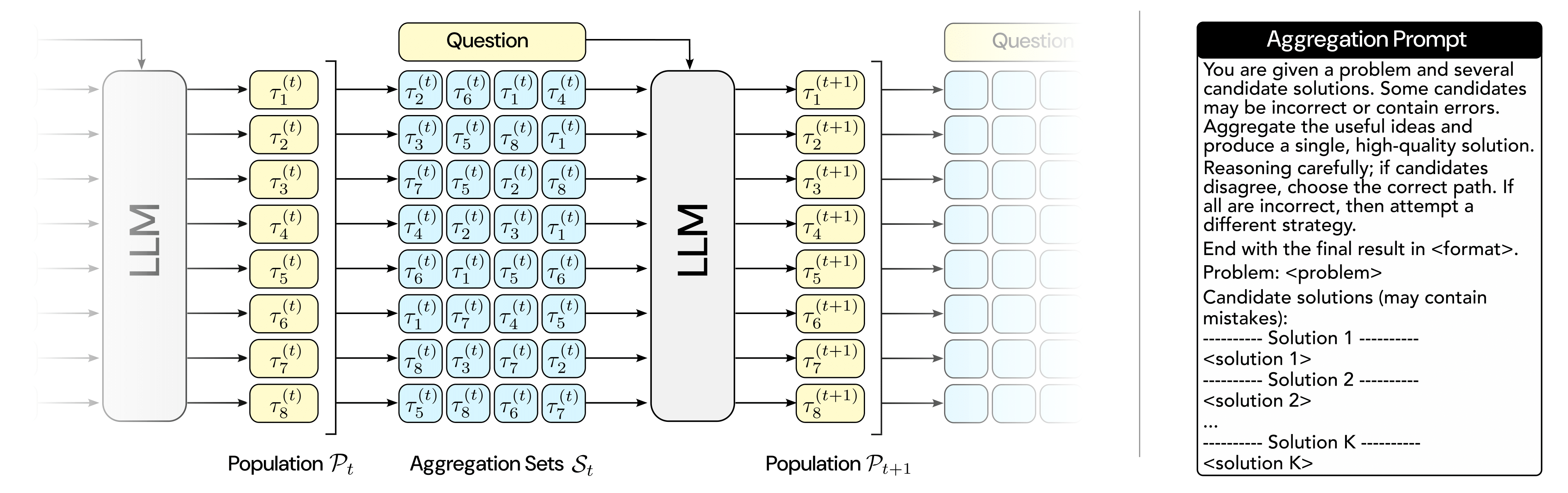
Population of trajectories. At any given step $t$, RSA maintains a population of $N$ independent candidate solutions $\mathcal{P}_t$. The initial population $\mathcal{P}_1$ is generated by sampling $N$ responses for query $\mathbf{x}$ using the LLM $p_{\theta}$.
Subsampling. We form $N$ aggregation sets of $K$ candidates, where each set is sampled uniformly without replacement from the population.
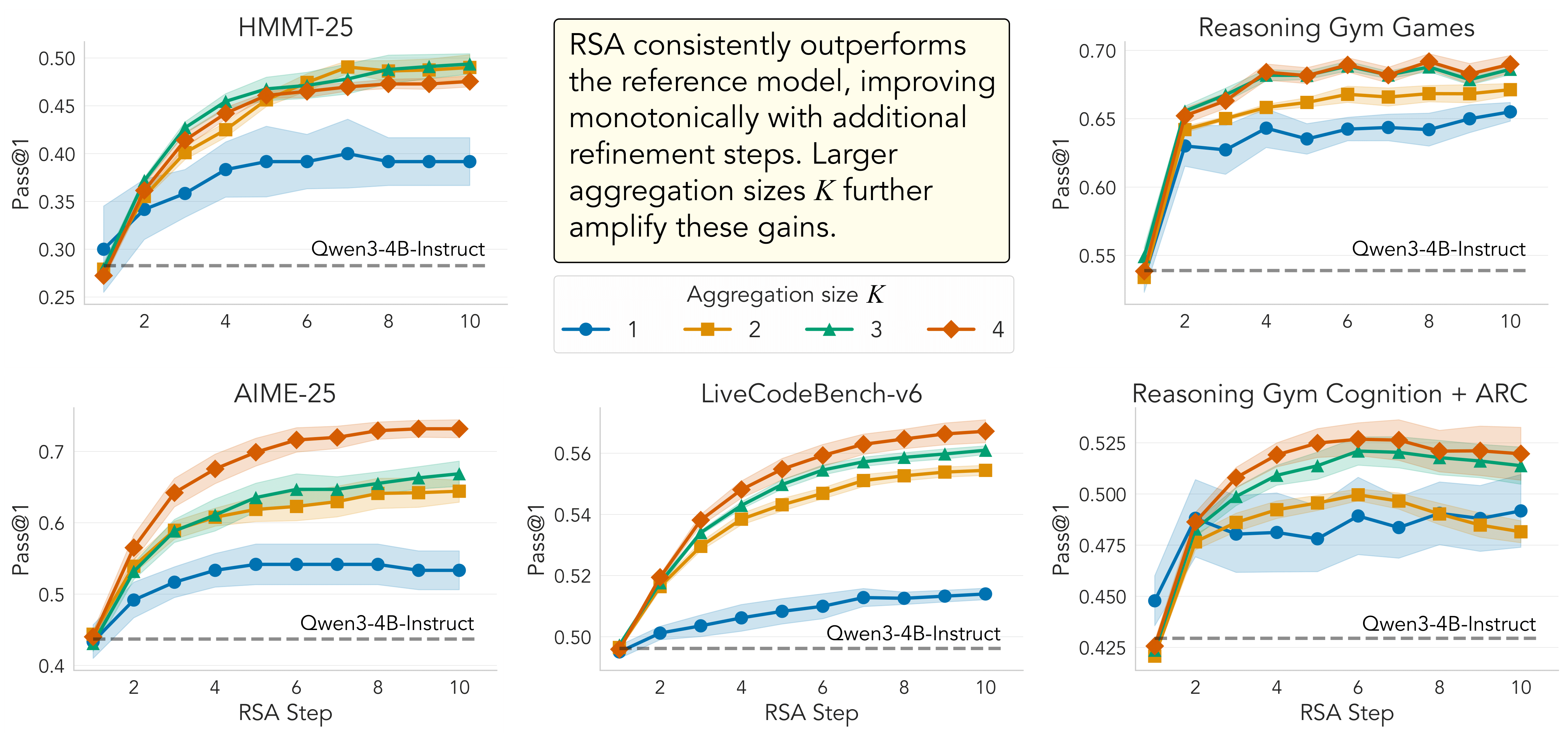
Aggregation. Each set of candidates and the query $\mathbf{x}$ is formatted using an aggregation prompt directing the LLM $p_{\theta}$ to generate a refined response $\tau_{i}^{(t+1)}$, forming a new population of candidates $\mathcal{P}_{t+1}$. RSA recursively updates the population $\mathcal{P}_t$ using subsampling and aggregation for $t=1,\dots,T-1$. This sequential loop is expected to allow errors and inconsistencies to be gradually pruned away during aggregation, while preserving favorable reasoning patterns. Consequently, we expect overall diversity within the population to generally decrease as $t$ increases, accompanied by a monotonic improvement in success rate.
Termination. Given the final population of candidate solutions $\mathcal{P}_T$, the solution is obtained either by randomly sampling from this population or by majority voting. We use uniform random sampling in all our experiments, to evaluate our method without any special selection mechanism.

Results

We evaluate RSA across four benchmark categories:

Math. We use AIME-25 and HMMT-25 from MathArena, each containing $30$ challenging competition-level math problems.
General reasoning. We construct two datasets with $100$ problems each from Reasoning Gym, using tasks from the games category (long-term planning), and cognition + ARC categories (pattern recognition).
Code generation. We use LiveCodeBench-v6 which contains 1055 problems.
Knowledge-based reasoning. We use SuperGPQA, a graduate-level knowledge-based reasoning benchmark, to test effectiveness of RSA on tasks requiring factual recall. Given the large dataset size, we evaluate on 1000 randomly chosen multiple-choice questions.

Comparison with other test-time scaling methods

RSA outperforms several test-time scaling methods, including both sequential scaling methods like self-refinement and parallel scaling methods like majority voting and Best-of-N with self-verification. RSA also beats single step self-aggregation (setting $T=1$) by a considerable margin, highlighting that sequential improvement is an important component of this method.

RSA leads to monotonic improvements with more compute

We report Pass@$1$ scores for RSA and other test-time scaling baselines for Qwen3-4B-Instruct-2507. RSA results obtained with aggregation size $K=4$, population size $N=16$, run for $T=10$ steps. Majority-voting and rejection-sampling are budget-matched with RSA. Results are averaged over 4 seeds for all tasks except SuperGPQA, where we use 1 seed.

RSA yields consistent gains across different models

We apply RSA to a diverse set of instruction-tuned models spanning a wide range of parameter counts, architectures, and reasoning abilities, including long chain-of-thought “thinking” models, sparse Mixture-of-Experts (MoE) architectures, and hybrid state-space models.

RSA leads to substantial improvements on all tasks across a wide range of models.

RSA scales effectively with more compute

An ideal test-time scaling method yields monotonic improvements with more compute. We scale RSA along two axes: the sequential depth (number of iterations) and aggregation set size (number of candidates aggregated). We see that RSA scales effectively with both hyperparameters across tasks. Moving from $K=1$, which corresponds to single-trajectory refinement, to $K=2$ results in a large improvement, highlighting that aggregating multiple solutions is a crucial component.

RSA leads to monotonic improvement with more compute along two axes: scaling number of iteration steps and scaling the aggregation set size. Results on Qwen3-4B-Instruct-2507.

Aggregation-aware RL

Reinforcement learning (RL) improves the model’s ability to directly generate correct solutions, but does not explicitly teach the model how to aggregate multiple candidate solutions. As we show in our results, this mismatch between the training objective and the test-time strategy can result in worse performance compared to the base (reference) model when using RSA.

To better align training and inference, we formulate the task of aggregation as an RL problem. The reference model $p_{\theta}$ generates a set of candidate reasoning chains given a problem. Next, the model is trained to produce a single correct reasoning chain given the problem and the set of candidate reasoning chains. To achieve this in practice, we create an aggregation-aware training dataset consisting of two types of prompts: (1) Standard prompts, containing only the problem, to train the model to propose good initial candidate reasoning chains; and (2) aggregation prompts, which include the problem along with $K$ candidate solutions from the reference model, formatted with the same aggregation prompt used for RSA.

Our proposed aggregation-aware RL improves RSA performance

Performance across RSA steps for the base, standard RL, and aggregation-aware RL policies with Qwen3-4B-Instruct-2507. Standard RL training generally hurts performance when using RSA, whereas aggregation-aware training leads to marked improvement on most tasks..